| 1、
|
设正态总体的方差 σ
2 为已知，问抽取的样本容量n为( )，才能使总体均值 μ 的置信度为0.95的置信区间长不大于L |
|
|
| 2、 |
在一批铜丝中，随机抽取9根，测得其抗拉强度为578，582，574，568，596，
572，570，584，578 设抗拉强度服从正态分布，则 σ
2 的置信为0.95的置信区间为( )
|
|
|
| 3、 |
在一批螺丝钉中，随机抽取16个，测其长度(cm)为：2.23，2.21，2.20，2.24，2.22，2.25，
2.21，2.23，2.24，2.25，2.25，2.21，2.24，2.23，2.25，2.22 设螺钉长度服从正态分布
则总体均值 μ 的90%的置信区间为( )，已知 σ=0.01 |
|
|
| 4、 |
在一批螺丝钉中，随机抽取16个，测其长度(cm)为：2.23，2.21，2.20，2.24，2.22，2.25，
2.21，2.23，2.24，2.25，2.25，2.21，2.24，2.23，2.25，2.22 设螺钉长度服从正态分布
则总体均值 μ 的90%的置信区间为( )，其中 σ 未知 |
|
|
| 5、 |
设二正态总体 X，Y 中分别抽取容量为16和10的两个样本，求得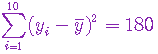
，
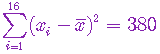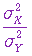，则方差比  的95%置信区间为(
) |
|
|
|
|
|
|
