| 1、
|
如果两个随机变量X与Y独立,则( )也独立 |
|
|
| 2、 |
已知二维随机向量(X,Y)服从矩形区域D上的均匀分布,
其中D={ ( x , y ) = a ≤ x ≤ b , c ≤ y ≤ d }
则随机变量 X 与 Y 是( ) |
|
|
| 3、 |
"已知二维随机向量(X,Y)服从区域D上的均匀分布,
其中D={(x,y): x2
+ y2
≤ 2x }则随机变量X与Y是( ) |
|
|
| 4、 |
设(X,Y)是二维连续型随机向量,联合分布密度为
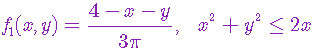
则X与Y是( ) |
|
|
| 5、 |
设(X,Y)是二维连续型随机向量,联合分布密度为
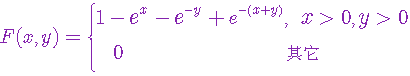
则X与Y是( ) |
|
|
|
|
|
|
